Wie verwenden heute das Wort Computer meistens ohne die Assoziation, dass diese Maschine „rechnet“, also mit mathematischen Methoden ein Problem löst, das zu einem numerischen Ergebnis führt. Jedoch war genau das die Motivation die ersten elektronischen Computer zu bauen. Das zugrundeliegende Problem ist, dass viele Probleme in den Ingenieurwissenschaften, der Physik, Chemie, Geologie, Meteorologie und anderen Naturwissenschaften sich entweder nicht exakt lösen lassen, sondern nur näherungsweise numerisch, oder die exakte Lösung sehr viele, manuell schwer zu bewältigende Rechenschritte erfordert. Bis 1951 waren alle elektronischen Computer genau für diese Aufgaben entwickelt worden. Mit dem Aufkommen der kommerziellen Datenverarbeitung verschob sich das Verhältnis der verkauften Computer zugunsten der Rechner für Geschäftsanwendungen aber bis heute werden die leistungsfähigsten Rechner für numerische Berechnungen verwendet.
Seit den ersten PC oder auch Heimcomputern – diese Differenzierung entstand erst als IBM mit der Entwicklung des IBM PC den kommerziellen Markt der persönlichen Computer erschloss – wurden auch die unterschiedlichsten dieser Systeme für Rechenaufgaben genutzt. Ich selbst habe in den frühen 1980er Jahren während meines Studiums auf diese Möglichkeit zurückgegriffen, nicht ohne auch mit dem Teil zu spielen.
In Erinnerung daran möchte ich heute einen Exkurs in die Rechenleistung der damaligen Systeme unternehmen. Das ist mir persönlich mit einer realen Hardware nur mit meinem C64 möglich. Jedoch erlauben die vielfältigen Rechnersimulationen einen Vergleich auch heute noch. Dabei ist die eigentliche Hardware verhältnismäßig uninteressant. Nachdem seit Ende der 1940er Jahre im Wesentlichen alle Rechner turing-vollständig sind, ist es am Ende immer eine Frage des Algorithmus und der genutzten Software wir exakt das numerische Ergebnis ermittelt werden kann. Darum möchte ich heute drei „Systeme“ gegeneinander antreten lassen, um deren Leistungen in einem einfachen Test zu vergleichen.
Eine wunderbare Quelle für – mal mehr, mal weniger – herausfordernde Programmieraufgaben ist eine meiner Lieblingswebsites Rosetta Code. Dort habe ich ausgehend der Programmieraufgabe Runge-Kutta method die Lösung für den C64 entwickelt und dann portiert.
Mit den PC, die seit ca. 1975 zur Verfügung standen, bot sich als Entwicklungsumgebung für eine portierbare Programmierung effektiv nur BASIC an. Diese heute so viel gescholtene Programmiersprache war damals der de-facto Standard und bot etliche Vorteile:
- Betriebssystem und Entwicklungsumgebung konnten gebündelt und in ein ROM gebrannt werden, um einen Rechner anzubieten, der in Sekundenschnelle arbeitsbereit war und den Fokus auf das Programmieren und nicht das Drumherum legte
- BASIC war sehr deutlich durch FORTRAN beeinflusst und so war ihm das Lösen numerischer Aufgaben quasi mit in die Wiege gelegt worden
- Viele numerische Verfahren erfordern keine komplexen Algorithmen mit vielen Zeilen Code, sondern das oft wiederholte Ausführen von Rechenschritten mit möglichst hoher numerischer Genauigkeit
Darum sehen wir uns hier zunächst nur Lösungen unter Basic an und kommen auf andere Programmiersprachen ein Andermal zurück.
Das Runge-Kutta-Verfahren ist ein etabliertes, relativ altes aber auch heute noch genutztes Verfahren zur numerischen Lösung von Differentialgleichungen. Ohne hier zu erklären, was Differentialgleichungen genau sind, traue ich mich zu sagen, dass sie die Masse der zu lösenden Aufgaben in der numerischen Mathematik bilden und einer der Gründe für die Entwicklung von elektronischen Rechnern waren. Für sehr viele Aufgabenstellungen, zum Beispiel in der Physik, gibt es präzise Differentialgleichungen zur Beschreibung des Phänomens aber keine mathematisch exakten Lösungen dafür. Als ein Beispiel sei hier die ballistische Kurve, also die Flugbahn eines realen Geschosses, genannt. Hier gibt es eine exakte Lösung nur, wenn man relevante Faktoren außer acht lässt, wie etwa Luftwiderstand, Rotation des Geschosses und den Einfluss der Erdrotation. Der ENIAC, einer der ersten elektronischen Rechner überhaupt, wurde unter anderem zu diesem Zweck entwickelt und durch das US-Militär finanziert.
Hier wollen wir weniger martialisch sein und auf die numerische Lösung einer einfachen Differentialgleichung beschränken, deren exakte Lösung bekannt ist. Das ist logischerweise erforderlich um die Qualität der Berechnung durch den Vergleich zwischen exakter und genäherter Lösung zu bestimmen. Die Aufgabenstellung ist bei Rosetta Code sehr gut beschrieben. Ich gehe von der Lösung mit BBC BASIC als Referenz aus, weil sich die in dieser wunderbaren Entwicklungsumgebung unmittelbar nachvollziehen lässt.
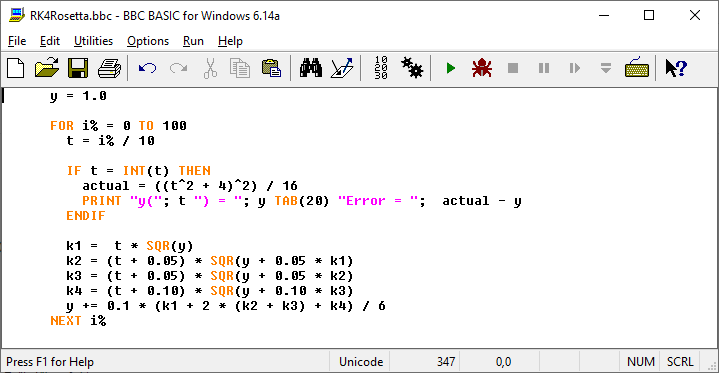
Das Programm zweigt das gleiche Ergebnis wie bei Rosetta-Code:
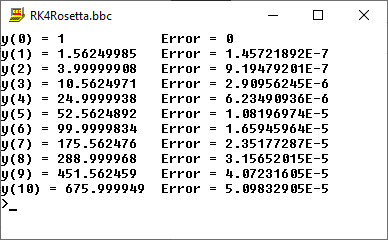
Wenn ich jetzt dieses Programm in die Vergangenheit zurück portieren möchte, treten ein paar Probleme auf:
- Ältere BASIC-Dialekte kannten keine IF-ENDIF-Konstrukte
- Die Wirkung des PRINT-Befehls, insbesondere mit numerischen Variablen, war im angezeigten Ergebnis unterschiedlich
- Bei BBC-BASIC und den meisten aktuellen BASIC-Dialekten wird das %-Zeichen an einer Variablen verwendet, um eine Integer-Variable zu definieren. In der Vergangenheit waren das teilweise andere Zeichen oder diese Option fehlte ganz
- Ein relativ neuer Operator wie das y += … (bedeutet y = y+ … )fehlte bei älteren BASIC-Dialekten meistens
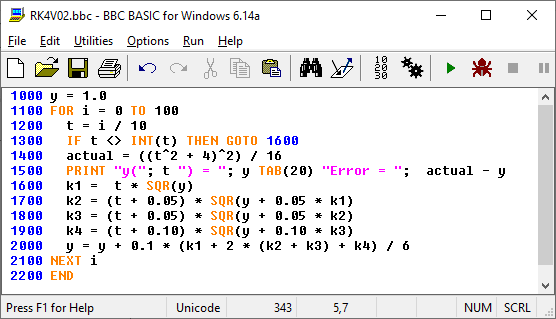
Der „Downgrade“ unter BBC-Basic versucht die genannten Klippen zu umschiffen, ohne den PRINT-Befehl zu verändern. Und die erste Station ist natürlich der C64.
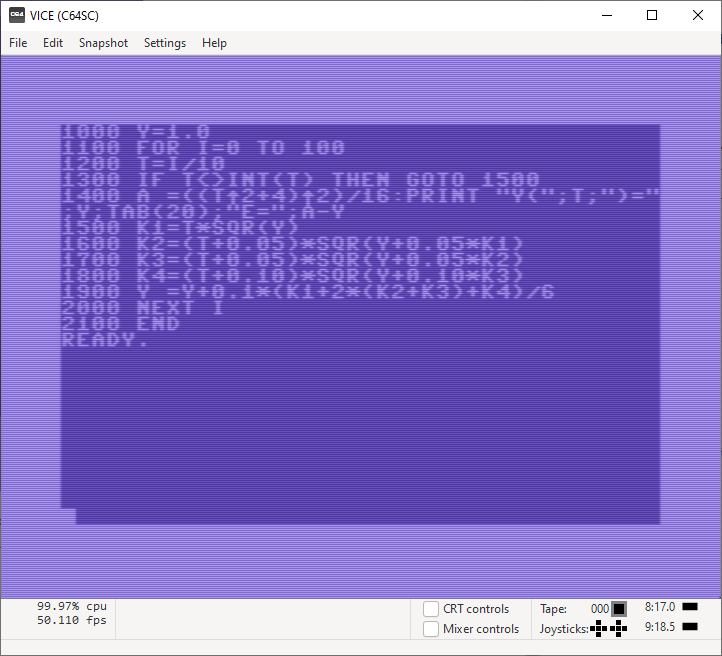
Der Code ist weitgehend unverändert, bis auf das PRINT-Statement. Ganz erheblich länger ist allerdings die Laufzeit, sogar auf dem simulierten C64, der allerdings auch versucht die Originalgeschwindigkeit zu simulieren. Das numerische Ergebnis des Funktionswerts weicht gar nicht so sehr von den Referenzwerten ab, jedoch ist der ausgewiesene Fehler leicht unterschiedlich, was u. a. daran liegt, dass auch die Berechnung des Vergleichswerts auf Basis der exakten Lösung mit einer numerischen Ungenauigkeit behaftet ist.
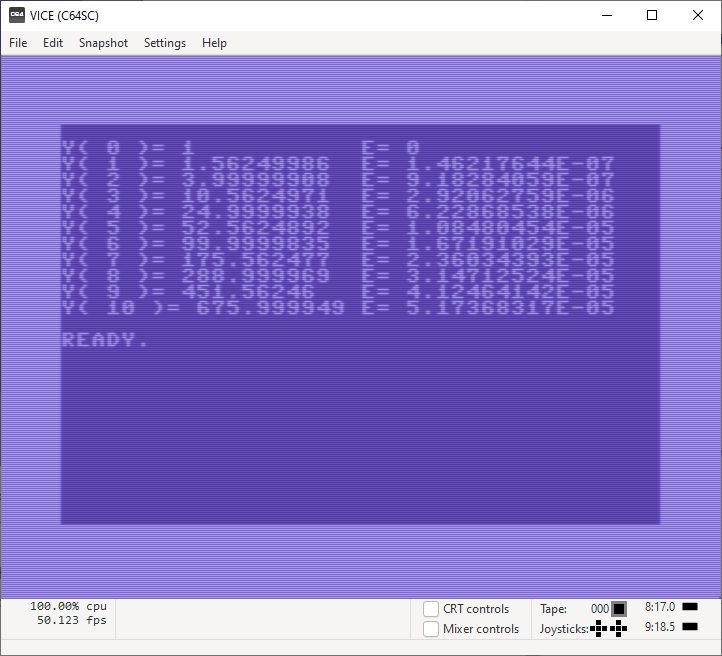
Für einen „Spielcomputer mit einem oft belächelten BASIC ist das Ergebnis gar nicht so schlecht finde ich. Als nächstes schicken wir jetzt Microsoft ins Rennen und zwar auf dem SIMH-Altair unter CP/M mit dem sehr weit entwickelten M-BASIC in der Version 5.29 aus der wunderbaren Sammlung von Altair Programming Languages von Peter Schorn’s Home Page.
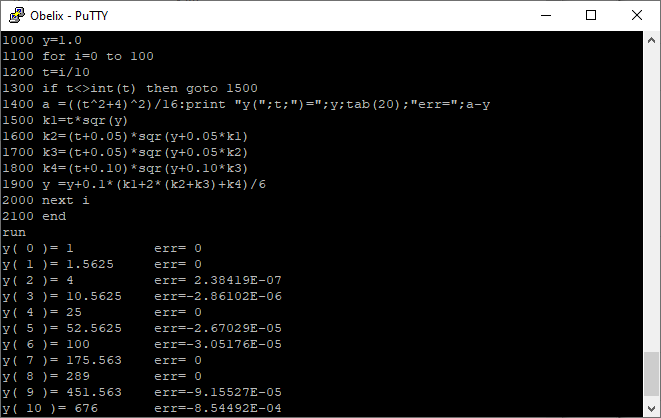
Das Programm konnte ohne Veränderungen vom C64 übernommen werden und das Ergebnis überrascht insofern, als für x=2, 4, 6, 8 und 10 die exakten Werte entsprechend der exakten Lösung ausgegeben werden – was auf eine verbesserte Arithmetik in der Software schließen lässt.
Als letzten Kandidaten lassen wir jetzt den CBASIC Compiler CB-80 von Digital Research auflaufen, der sich auf der gleichen Disk aus Peter Schorns Sammlung befindet. Der Code wurde nur im PRINT-Statement angepasst, um eine entsprechend formatierte Ausgabe zu erhalten. Das verwendetet USING-Statement findet sich auch in vielen anderen BASIC-Dialekten wieder.
Anders als bei den bisher benutzten BASIC-Interpretern muss hier der Source-Code zwingend compiliert und gelinkt werden, was der Aufruf CB80 [Sourcefile ohne Extension] und LK80 mit dem gleichen Parameter bewirkt.
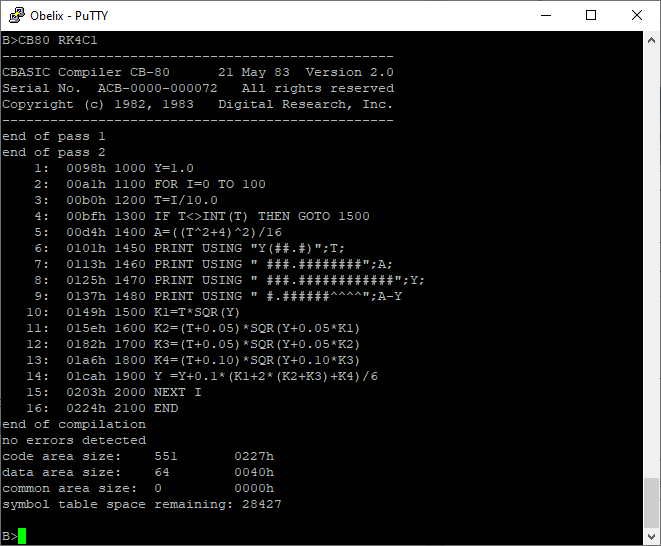
Und gleich hinterher den zum Compiler mitgelieferten Linker aufrufen:
Dadurch wird eine Ausführbare Datei (.COM) erzeugt, die als solche aufgerufen werden kann:
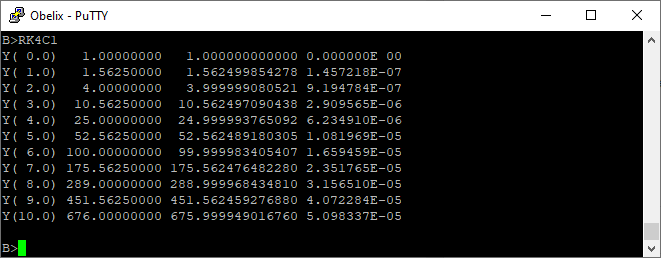
Neben der rasanten Ausführungsgeschwindigkeit (Compiler halt) überrascht CB80 durch die große Genauigkeit der Fließkomma-Variablen.
Im Ergebnis kann man feststellen, dass die Systeme der späten 1970er und frühen 1980er Jahre sehr wohl in der Lage waren numerische Aufgaben zu bewältigen. Dabei gab es durchaus Unterschiede:
- Die Numerik des C64 ist eher schlechter als die der Konkurrenten
- Die Ausführungsgeschwindigkeit kann so nicht verglichen werden, da die SIMH-Simulation des Altairs wesentlich schneller arbeitet als die reale Hardware das getan hätte. Allerdings weiß ich aus eigener Erfahrung, dass numerische Berechnungen auf dem C64 schon immer recht langsam waren, was auch an der Architektur des verbauten 6502-Prozessors lag
- Das Microsoft-Basic ist für damalige Verhältnisse sehr leistungsfähig und absolut geeignet, numerische Ergebnisse zu erhalten
- Der CB80-Compiler geht da noch deutlich weiter. Der Sprachumfang ist wesentlich erweitert gegenüber den anderen Programmen. So gibt es etwa mehrzeilige Funktionen, sogar mit lokalen Variablen, Includes, Einbindung von Assembler-Code, verschachtelte IF-Statements und eine WHILE-Schleife
